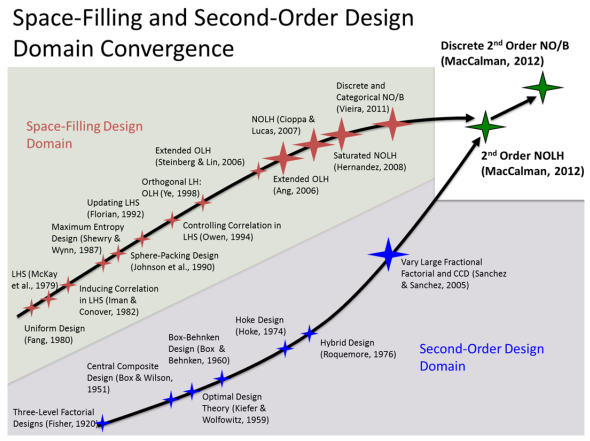
To better understand the complex nature of a system, analysts need efficient experimental designs that can explore high-dimensional simulation models with multiple outputs. These simulation models are critical to the early phases of system design and involve complicated outputs with a wide variety of linear and nonlinear response surface forms. The most common response surface form for analyzing complex systems is the second-order model. Traditional designs that fit second-order response surface models do not effectively explore the interior of the experimental region and cannot fit higher-order models. To address this gap, I created a genetic algorithm that constructs space-filling designs with minimal correlations between all second-order terms for a mix of continuous and discrete factor types. These designs are specifically suited to fit the second-order model with excellent space-filling properties and are flexible enough to fit higher-order models for a modest number of factors; these high-order terms are what characterize the system complexities. My research enables the simulation analysis and system design community to better understand the complex nature of multiple simulation outputs. The following figure depicts my contribution to the statistical body of knowledge.
See this link for my dissertation: Alex MacCalman's Dissertation
See this link for a video of my dissertation defense: Dissertation Video
See this link for my genetic algortihm code respository: GitHub Repo